Potenciação
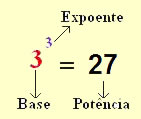
Podemos dizer que potenciação representa uma multiplicação de fatores iguais, se temos a seguinte multiplicação: 2 x 2 x 2 x 2 x 2 x 2, podemos representá-la usando a potência 26, onde 2 é a base e 6 o expoente (Leia: dois elevado a sexta potência).
O expoente possui um papel fundamental na potenciação, pois ele é quem define quantas vezes a base será multiplicada por ela mesma. Observe:
26 = 2 x 2 x 2 x 2 x 2 x 2 = 64
42 = 4 x 4 = 16
53 = 5 x 5 x 5 = 125
102 = 10 x 10 = 100
122 = 12 x 12 = 144
35 = 3 x 3 x 3 x 3 x 3 = 243
63 = 6 x 6 x 6 = 216
Casos de potenciação
Todo número diferente de zero e elevado a zero é um.
20 = 1
30 = 1
100 = 1
40 = 1
1250 = 1
Todo número diferente de zero e elevado a um é o próprio número.
21 = 2
31 = 3
151 = 15
201 = 20
121 = 12
Base zero e qualquer número no expoente, o resultado será zero.
05 = 0
012 = 0
0100 = 0
07 = 0
025 = 0
Base negativa e expoente ímpar, resultado negativo.
(-3)3 = (-3) x (-3) x (-3) = -27
(-4)5 = (-4) x (-4) x (-4) x (-4) x (-4) = -1024
(-2)7 = (-2) x (-2) x (-2) x (-2) x (-2) x (-2) x (-2) = -128
Base negativa e expoente par, resultado positivo.
(-2)4 = (-2) x (-2) x (-2) x (-2) = + 16
(-6)2 = (-6) x (-6) = + 36
(-7)2 = (-7) x (-7) = + 49
Base é um número racional (fração): devemos elevar ao expoente indicado o numerador e o denominador da fração.
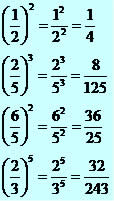
Quando o expoente é um número negativo: invertemos a base e mudamos o sinal do expoente para positivo.
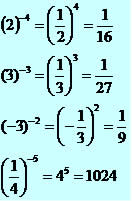
Uma importante aplicação de potenciação é a notação científica, usada para expressar valores muito grandes ou muito pequenos. A notação é usada por cientistas, como astrônomos, físicos, biólogos, químicos entre outros.
Exemplos:
6 120 000, podemos representá-lo usando a seguinte notação decimal 6,12 * 106
0,00012, pode ser representado por 1,2 * 10-4.
Fonte:http://www.alunosonline.com.br/matematica/potenciacao.html.
Radiciação
Uma raiz nada mais é que uma operação inversa à potenciação, sendo assim, ela é utilizada para representar, de maneira diferente, uma potência com expoente fracionário.
Exemplos
Raiz com índice par
Para um número real a positivo, com n sendo um número natural par e positivo, maior que 1, tem-se um b, tal que, se ![\sqrt[n]{a} = b](http://www.infoescola.com/wp-content/plugins/latex/cache/tex_130de162c6033de1e69803db4ba5dc23.gif) , então bn = a, onde a é o radicando, n é o índice, b é raiz e √ é o radical. Com
, então bn = a, onde a é o radicando, n é o índice, b é raiz e √ é o radical. Com 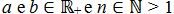 .
.
![\sqrt[n]{a} = b](http://www.infoescola.com/wp-content/plugins/latex/cache/tex_130de162c6033de1e69803db4ba5dc23.gif) , então bn = a, onde a é o radicando, n é o índice, b é raiz e √ é o radical. Com
, então bn = a, onde a é o radicando, n é o índice, b é raiz e √ é o radical. Com
Observação: quando o índice não aparecer no radical, isso indica que n = 2 e teremos uma raiz quadrada.
Exemplos:

Raiz com índice ímpar
Sendo a um número real, positivo ou negativo, com m sendo um número natural ímpar e positivo, maior que 1, tem-se um b, tal que, se ![\sqrt[m]{a} = b](http://www.infoescola.com/wp-content/plugins/latex/cache/tex_dc2c5e72d82cbe4193c42ac1d4350a19.gif) , então bm = a, onde a é o radicando, m é o índice, b é raiz e √ é o radical. Com
, então bm = a, onde a é o radicando, m é o índice, b é raiz e √ é o radical. Com 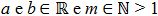 .
.
![\sqrt[m]{a} = b](http://www.infoescola.com/wp-content/plugins/latex/cache/tex_dc2c5e72d82cbe4193c42ac1d4350a19.gif) , então bm = a, onde a é o radicando, m é o índice, b é raiz e √ é o radical. Com
, então bm = a, onde a é o radicando, m é o índice, b é raiz e √ é o radical. Com
Nesse caso é possível obtermos raízes negativas dentro do conjunto dos números reais (ℝ).
Exemplos:
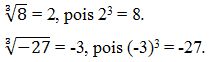
Propriedades
- Para o radicando que tenha, como resultado de uma fatoração, expoente igual a seu índice, então este radicando é igual à raiz procurada.
 Exemplos:
Exemplos: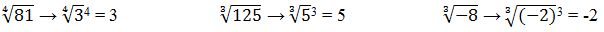
Podemos dividir o radicando e o índice por um mesmo número real, desde que este seja diferente de zero e maior que um, e divisor comum do radicando e do índice. 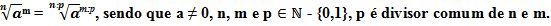
Exemplos:
- Para resolvermos a raiz m-esima de uma raiz n-ésima, multiplicamos os índices entre si mantendo intacto o radical interno.
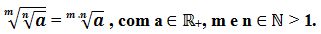 Exemplos:
Exemplos:
- A raiz n-ésima de um produto é igual ao produto das raízes n-ésimas.
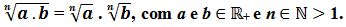 Exemplos:
Exemplos:
- A raiz n-ésima de um quociente (divisão) de a por b é igual ao quociente entre as raízes n-ésimas.
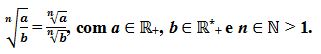
- Exemplos
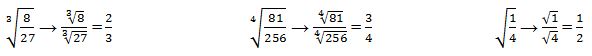
Fonte:http://www.infoescola.com/matematica/radiciacao/
![\sqrt[4]{2^3} = 2^{\frac{3}{4}}](http://www.infoescola.com/wp-content/plugins/latex/cache/tex_b30b3df7511dc05b2c6a7b8a346fa7aa.gif)

![\sqrt[n]{a^m} = a^{\frac{m}{n}}](http://www.infoescola.com/wp-content/plugins/latex/cache/tex_cdd70cbc67c0c3af89bbc72fa204239d.gif)
mt bom
ResponderExcluirEu quero saber quanto é (6elevado a quinta potência×6⁴÷6³.Poderiam por favor me responder?
ResponderExcluir